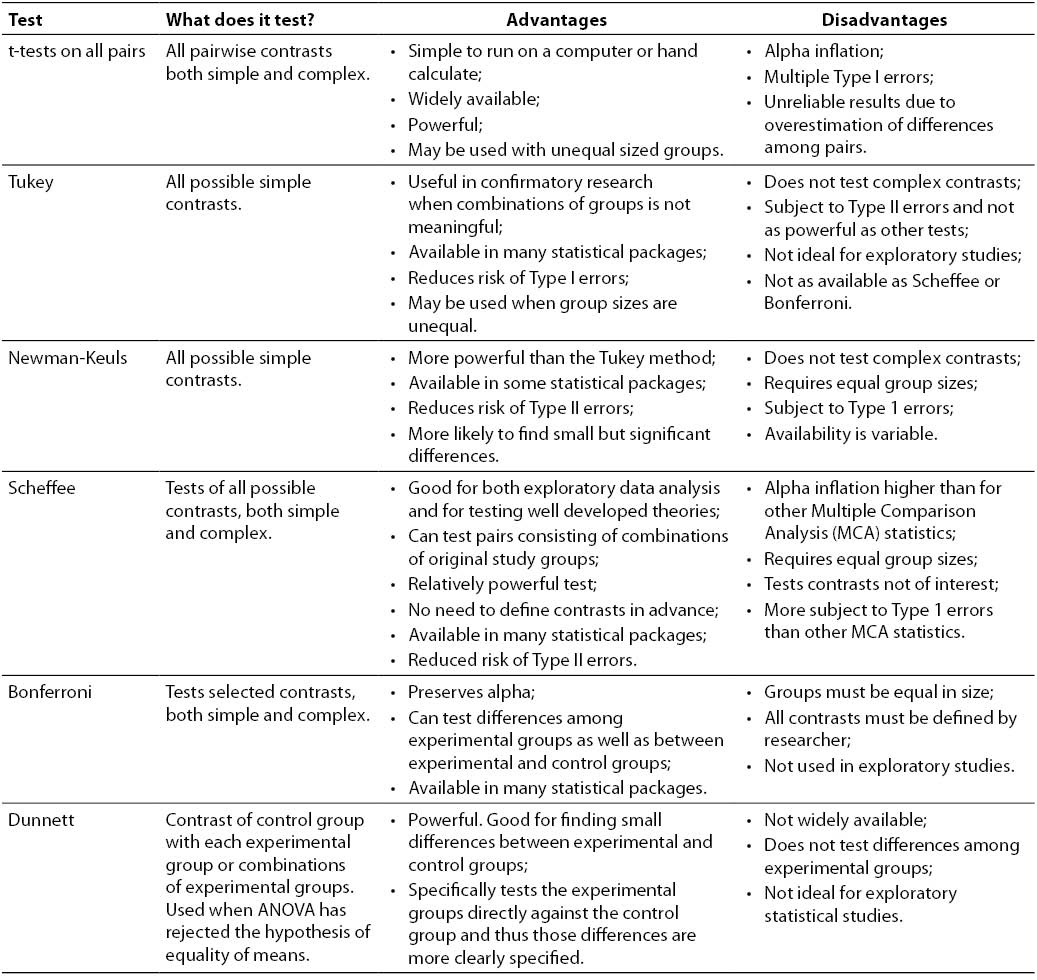
Use of multiple comparison analysis tests
Once an Analysis of Variance (ANOVA) test has been completed, the researcher may still need to understand subgroup differences among the different experimental and control groups. The subgroup differences are called “pairwise” differences. ANOVA does not provide tests of pairwise differences. When the researcher needs to test pairwise differences, follow-up tests called post hoc tests are required.
ANOVA output does not provide any analysis of pairwise differences, so how shall the researcher investigate differences among the various subgroups tested with ANOVA? The first approach that comes to mind is to perform a number of t-tests between each of the pairs of interest. This is not a good approach for two reasons: First, doing repeated statistical tests on the same data – which is what performing t-tests on each pair of interest does – causes alpha inflation (1). Second, the results will still be uninterpretable because individual t-tests can examine only two groups at a time. Each of the subgroups within an ANOVA has its own mean. The total number of means (i.e. the count of means, one for each of the experimental and control groups) is excluded from analysis when repeated t-tests are used to examine the pairwise differences from an ANOVA. Ignoring the fact that there are many more subgroup means in the ANOVA will artificially raise the number of pairwise differences that are significant, and worse, the individual pairwise t-statistics will be larger when some subgroups are excluded from the post hoc testing. Therefore, using t-tests to examine pairwise differences is likely to overestimate the size of the individual t-tests. This means that the sum of t-values from all the pairwise t-tests will often exceed the value of the t-statistic produced by one of the multiple comparison analysis statistics (2). As a result, performing multiple t-tests will lead the researcher to a higher probability of making a Type I error. That is, the researcher is much more likely to report significant differences between some of the pairs that have no real difference (1).
Performing multiple pairwise t-tests leads to another problem. The researcher may wish to test differences between one or more study groups and a set of combined study groups. Pairwise t-tests cannot perform that kind of analysis. However, there are a set of multivariate statistics that overcome all the limitations of the pairwise t-test approach. This category of statistics is called multiple comparison analysis. One of the multiple comparison analysis statistics should be used to examine pairwise and subgroup differences after the full ANOVA has found significance. The key tests of pairwise differences include: Bonferroni, Sheffèe, Tukey, Newman-Keuls and Dunnett.
Each of the multiple comparison analysis (MCA) tests has its own particular strengths and limitations. Some will automatically test all of the pairwise comparisons, others allow the researcher to limit the tests to only pairs or subgroups of interest. Each approach has implications for alpha inflation and for the kind of answers the researcher can derive from the test. Therefore, the choice of an MCA statistic, as all choices about which statistic to use (3), should be based on the specific research questions. For example, the researcher may have one experimental group of particular interest that should be compared separately against each of the control groups. Alternatively, the researcher may want to compare one experimental group against a combination of all the control groups, or against only some of the control groups, or even against one or more of the other experimental groups.
Many different situations occur in research that can affect the choice of a multiple comparison test (3). For example, the groups may have unequal sample sizes. One multiple comparison analysis test was specifically developed to handle unequal groups. Power may be an issue in a study, and some tests have more power than others. Tests of all comparisons will be important in some studies while other studies require testing only of predetermined combinations of the experimental or control groups. When special circumstances affect the specific pairwise analyses needed, the choice of a multiple comparison analysis test must be controlled by the ability of the specific statistic to address the questions of interest and the type of data to be analyzed.
Categories of contrasts
A contrast is a test of the difference between the means of two groups from the ANOVA. There are two categories of contrasts among the groups tested by ANOVA, simple and complex. A simple contrast is a test of the difference between any two pairs, such as Experimental Group 1 and Control Group 2. A complex contrast is a test of the difference between combinations of groups. An example of a complex contrast is a test of the difference between a subgroup created by combining Experimental Groups 1, 2 and 4 combined, and a subgroup created by combining Control Groups 1 and 3. The purpose of ANOVA is to either test theory or to generate theory, and multiple comparison analysis may be used to support either purpose.
Tests for comparing pairs
The Tukey method
Tukey’s multiple comparison analysis method tests each experimental group against each control group. The Tukey method is preferred if there are unequal group sizes among the experimental and control groups. The Tukey method proceeds by first testing the largest pair-wise difference. Tukey uses the “q” statistic to determine whether group differences are statistically significant. The “q” statistic is obtained by subtracting the smallest from the largest mean, and dividing that product by the overall group standard error of the mean (4). The overall group standard error of the mean divided by the sample size is known as the Mean Square Within (MSw) and is a satistic provided by the ANOVA output in virtually all statistical analysis programs (5). The q value can be compared to the values on a table of q-values to determine if the q-value from a particular pair exceeds the critical q-value needed to achieve statistical significance. If the q value meets or exceeds the critical value, that pair’s difference is statistically significant.
Note: it is common to use one tailed tests because the group means are already known from the ANOVA.
If the difference in means of the first pair was significant (which will be the case if the overall ANOVA was significant), the next pair is tested. The pairwise tests are continued until the obtained q-value is not significant. No others need be tested because they will not be significant. Tukey uses a fairly conservative estimate of alpha. It tests all the contrasts as a family and thus has a bit less power to find differences between pairs. In this context, family refers to the familywise error rate (6). This term addresses the likelihood of making a Type I error and thus a false discovery. Family tests reduce the possibility of making a false claim of significance (6), and should be used when the consequences of falsely reporting a significant difference are greater than the consequences of not finding a difference. Family tests provide more confidence in the results because such tests make few Type I errors (5,7).
An example of a good use of the Tukey statistic is a study in which four different antibiotics were used to treat Multiple-Drug Resistant Staphyloccus Aureus (MRSA) infections. Assume that the control group is treated only with Vancomycin, the standard treatment drug, and that three new antibiotics constitute the three experimental groups. It is likely that the group sizes could be different, and that is one reason to use Tukey. However, the most important reason to use Tukey is that making a Type I error is a greater worry than a Type II error. The reason is that making a Type I error means the researcher draws the conclusion that one or more of the experimental drugs are more effective than Vancomycin. If the truth is that Vancomycin is equally or more effective than the experimental drugs, that Type I error has much greater consequences than making a Type II error. In this example, the Type I error would lead clinicians to use a less effective experimental drug, that also is likely to cost a great deal more than Vancomycin. The outcome would be more deaths and a higher treatment cost. However, drawing a Type II error merely leaves treatment protocols unchanged. Thus, Tukey’s conservative alpha may lead to more Type II errors, but it will help the researcher avoid a Type I error.
The advantages of the Tukey method are that it tests all pairwise differences, it is simple to compute, and reduces the probability of making a Type I error. It is also robust with respect to unequal group sample sizes. Its chief disadvantages are that it is less powerful than some other tests, and it is not designed to test complex comparisons.
The Newman-Keuls method
The Newman-Keuls method is very similar to the Tukey test, except that it considers separately the alpha of each of the possible contrasts. Thus, it is not a family contrasts test. Ultimately, this is a more powerful test than Tukey because it performs more pairwise comparisons. Thus, it is more likely to find some differences to be statistically significant. Initially, it performs the same pairwise comparisons that the Tukey test runs. For those first comparisons, it has the same power as the Tukey. However, it then runs tests of each of the group means against the grand mean. The cost to this increased power is that it is far more liable to make a Type I error. It should be noted that the critical value used for the Newman-Keuls decreases with each subsequent test whereas Tukey uses the same critical value for all tests. That is how Tukey conserves alpha while the Newman-Keuls method expends alpha in finding more contrasts to be statistically significant.
This statistic should be used in studies for which relatively small pairwise differences are important. Examples of this kind of study include almost any research into very new and poorly understood phenomena. For example, when the HIV epidemic was new and there were no drugs to treat the infection, even weak differences between treatment drugs were important. With no drugs to treat the infection, a drug that had any effect in prolonging life was important. With its greater power, the Newman-Keuls statistic would be more appropriate to use than a less powerful test such as Tukey. Also, in this example, a Type I error is not as harmful as rejecting an effective drug for an inevitably fatal disease when there is no alternative treatment. The history of treatment of lethal diseases such as cancer and AIDS shows that most people would rather take a chance on a drug that might not help – or might cause harm – than do nothing at all.
In summary, the Newman Keuls statistic is appropriate for studies in which even very small differences are important to find and where the consequences of a Type II error are worse than the consequences of a Type I error. This makes it a useful tool for new areas of science where not much is known about the phenomena of interest. This is the classic theory development research situation. Other statistics should be used for more developed areas of research, and when the differences must be relatively large to make the new treatment better than the existing treatment. Newman Keuls should be used with in studies that produce equal group size.
Tests for comparing multiple groups
The Tukey and Newman-Keuls tests are designed to test simple comparisons. When the researcher must test subgroups composed of combinations of experimental and control groups, other statistics which can test complex comparisons should be used. The most commonly used statistics in this category are the Scheffee, the Bonferroni and the Dunnett statistics.
The Scheffee method
The Scheffee method, tests all possible contrasts, simple and complex. If it is known in advance that all contrasts are going to be tested, the Scheffee method is slightly more powerful than all other two methods. If only selected contrasts are to be tested, a different test called the Bonferroni Multiple Analysis Test is the better method. Thus the Scheffee, like the Tukey test, is the more appropriate test to use when predicted differences are small, and the consequences of a Type II error outweigh the consequences of a Type I error. The Scheffee test assumes equal sized experimental and control groups in the ANOVA.
When the theory that predicts the group differences the researcher expects to find is not well developed or tested, the Scheffee method is preferred because it tests all possible comparisons. In situations where there is not sufficient prior research to have tested the theory that explains the ANOVA’s findings, a more exploratory data analysis is needed for the post hoc tests. The Scheffee is a good exploratory statistic because it tests all possible comparisons. As a result, it allows the researcher to observe which groups or combinations of groups produced the significant difference found in the original ANOVA test. This is one method of exploratory data analysis, which is a strategy for discovering previously unknown differences among study groups, or for discovering if hypotheses based on very limited theory can be supported.
If the theory is well developed, Scheffee may also be a good choice. Well developed theory should predict differences for all groups and combinations of groups. Given that Scheffee tests all possible differences, it is a good test of multiple propositions of the well developed theory. Even though it analyzes all possible comparisons, the Scheffee limits the problem of alpha inflation, as do all multivariate analyses. Using the Scheffee as a theory-testing statistic, the theory is confirmed when differences predicted by the theory are found by Scheffee. When theory predicts no differences between other groups, Scheffee confirms the theory when it finds no significant differences among those groups. The Scheffee test is ideal for testing the well developed theory because, with minimal alpha inflation, it tests all possible pairwise differences, including combinations of pairs.
The Scheffee test is also a good tool to use when theory is not sufficiently developed to confidently predict which pairs and combinations of pairs will be significantly different. The overall ANOVA can produce a significant F-test even when two or more groups within the analysis are not significantly different. It is often important to discover exactly which group differences produced the significant F-test. In this situation, to discover which groups within the ANOVA were significantly different, the researcher must perform multiple comparison analyses. For example, suppose four different antibiotics were tested for mortality rates among patients with necrotizing fasciitis. All the ANOVA can determine is if there were significant differences among the groups’ mortality rates. It cannot identify which drug produced the lowest mortality rates, or if two or three of the drugs were equivalent in effectiveness and one was ineffective. The Scheffee method provides that detailed information about each drug.
The Scheffee test allows the researcher to conduct a theory generation study by testing all possible contrasts to discover which are significant. This sort of research assists the researcher to make serendipitous findings from existing data and is part of the science of discovery in exploratory data analysis. Previously unknown differences can be detected and the researcher creates new theory by developing an explanation that accounts for the observed differences. Theory generated with this method should be tested in subsequent studies designed specifically to test the new theory. This is important because the probability of finding spurious relationships is higher in exploratory data analysis than in theory testing procedures (i.e. Type 1 errors are more likely to exist in this kind of research, and the discovered differences should be confirmed by subsequent studies).
Subsequent studies testing specific subgroup contrasts discovered through the Scheffee method should use the Bonferroni method which is more appropriate for theory testing studies. The Bonferroni method is less susceptible to Type I errors than the Scheffee method.
The Bonferroni (Dunn) method
Like the Tukey method, the Bonferroni method of multiple comparisons is a family contrasts comparison method, so it does not inflate alpha to the extent that other types of multiple comparison analyses (such as the Newman-Keuls method) do. Additionally, like the Scheffee method, the Bonferroni method can test complex pairs. However, the Bonferroni statistic is not a tool for exploratory data analysis. It requires the researcher to specify all contrasts to be tested in advance. The researcher must have sufficient theory about the phenomena of interest in order to know which contrasts to specify. As a result, this is a better test for confirming theory about the experimental group’s results than exploratory methods such as the Scheffee. Because Bonferroni limits the number of tests to those specified in advance by the researcher, it reduces the problem of alpha inflation. The great advantage of the Bonferroni method is that it reduces the probability of a Type I error by its limits on alpha inflation. However, it cannot make serendipitous discoveries and it therefore provides less information on differences among the groups because not all differences are tested.
The Dunnett method
The Dunnett method is useful for testing control group designs. It is a particularly powerful statistic and therefore it can discover relatively small but significant differences among groups or combinations of groups. The Dunnett method is quite useful when the researcher wishes to test two or more experimental groups against a single control group. It tests each experimental group’s mean against the control group mean. The other methods test each study group against the total group mean (i.e., the grand mean). This difference in testing approach makes the Dunnett method much more likely to find a significant difference because the grand mean includes all group means and thus mathematically it is less extreme than individual group means. The more extreme group means will produce larger mean differences than tests comparing one group mean to the grand mean. The Bonferroni method could be specified to test only the experimental groups against the single control group, but given that it compares study group means against the grand mean, it has less power than the Dunnett method.
Summary
There are a variety of post hoc tests available to further explicate the group differences that contribute to significance in an ANOVA test. Each test has specific applications, advantages and disadvantages (Table 1). It is therefore important to select the test that best matches the data, the kinds of information about group comparisons, and the necessary power of the analysis. It is also important to select a test that fits the research situation in terms of theory generation versus theory testing. The consequences of poor test selection are typically related to Type 1 errors, but may also involve failure to discover important differences among groups. Multiple comparison analysis tests are extremely important because while the ANOVA provides much information, it does not provide detailed information about differences between specific study groups, nor can it provide information on complex comparisons. The secondary analysis with these post hoc tests may provide the researcher with the most important findings of the study.
Potential conflict of interest
None declared.
Table 1. Comparison of different multiple comparison analysis statistics.